Technika cieplna – ćwiczenie laboratoryjne nr 7   (21.04.07) 

BADANIE PARAMETRÓW PRZEMIANY ADIABATYCZNEJ

4Inst-ADplusRys-27

  1. Matematyczno-fizyczny opis przemiany adiabatycznej.

Adiabatą nazywamy  przemianę, w której warunkiem koniecznym jest brak wymiany ciepła z otoczeniem. Jest to możliwe wówczas, gdy podczas tej przemiany ani ciepła nie doprowadzamy, ani też go nie odprowadzamy. Ponieważ  q = const (lub Q = const) wartość różniczkowego ciepła przemiany adiabatycznej wyniesie:

Jeśli przemiana ta jest odwracalna, spełnia ona również warunek braku przyrostu entropii

                                                                                                                 

Całkowanie równania (1) pozwala stwierdzić niezmienność entropii (). Dlatego też odwracalna przemiana adiabatyczna bywa nazywana przemianą izentropową lub ściślej przemianą adiabatyczno-izentropową. Przebieg przemiany przedstawiony jest na rys. 1 w układzie  p – υ, zwanym układem pracy, a na rys. 2 w układzie ciepła (T – s).

 

 

 


                       

 

υ   [m3/kg]
 
 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 


Rys. 1. Przemiana adiabatyczna na wykresie p – υ   (tzw. układ pracy).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 


 

                       

Rys. 2.  Adiabata na wykresie T – s  (tzw. układ ciepła).

 

Podstawą analitycznego ujęcia przebiegu przemiany adiabatyczno-izentropowej jest pierwsza zasada  termodynamiki  sformułowana  w 1842 r. przez  J. R. Mayera ( uściślona 5 lat później przez H. de Helmholtza). Poniżej wyprowadzimy pierwszy wariant równania adiabaty przy założeniu, że opis przemiany wyrazimy za pomocą  współrzędnych p – υ .

Z równania I zasady termodynamiki (tzw, pierwsza postać) i warunku cieplnego przemiany (dq = 0) wynika:

                                                                                                        (1)

gdzie:

.dq

-

elementarne ciepło przemiany [J/kg],

du    -   różniczkowy przyrost energii wewnętrznej ( du = cv dT) , [J/kg],

 

    dlz =  p dυ  -   elementarna praca zewnętrzna [ J/ kg],

    p               -   ciśnienie [ Pa = N/ m2],

    υ               -   objętość właściwa równa  υ = V/m , ,

    V,  m         -  objętość [m3]  i masa gazu [kg]

Ponieważ du = , więc

              .                

Równanie stanu gazu doskonałego (wariant chemiczny wykorzystuje uniwersalną stałą gazową a wersja techniczna  - indywidualną stała gazową Ri = R) ma postać:

                        .p υ =  R T                  [ J/ kg ],

R – indywidualna stała gazowa [ J/(kg K) ],

T – temperatura bezwzględna [ K ].

Powyższe równanie pozwala – po zróżniczkowaniu - wyznaczyć:

dT = d (p υ)/R,           czyli    

                                                                         (2)

Indywidualna stała gazowa [ J/( kg K)] może być ujęta tzw. wzorem Mayera:

 ,               więc

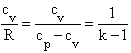                                                                         (3)  

Stosunek      jest tzw. wykładnikiem przemiany adiabatycznej ( w równaniu końcowym wystąpi jako wykładnik potęgi w członie z objętością właściwą).

Podstawiając wyrażenie (3) do równania (2) otrzymuje się:

              .

Mnożąc obie strony równania przez (k-1) uzyskujemy po redukcji wyrazów podobnych :

Dzieląc obie strony równania  przez iloczyn p.v otrzymamy równanie różniczkowe adiabaty:

                                                                                                                       

Jego całkowanie prowadzi do wyniku

              ,

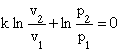i następnie:

p1 .υ1k    = p2 .υ2 k ,                                                                   (4)

co stanowi równanie adiabaty-izentropy w układzie p – υ ( tzw. układ pracy).

Krzywe ilustrujące  przemianę adiabatyczną  przedstawione zostały na rys. 1, 2.

            Równanie adiabaty możemy przedstawić również w postaciach odmiennych od równania (3), uwzględniających zmianę trzeciego czynnika czyli temperatury. W tym celu zależność (3) zapiszemy w  postaci ogólnej, wykorzystując równanie stanu:

            p .υ k 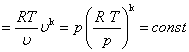                                                                          (5)

Z ogólnej postaci równania adiabaty (4) można uzyskać następujące zależności:

a)      zmienność objętości właściwej i temperatury:

T υ k-1 = const,  lub                                                 (6)

b)      zmienność ciśnienia i temperatury:

T k  p1 – k = const,  lub   

Równanie (6) może być podstawą do przewidywania kierunku zmiany temperatury przy sprężaniu (spadek objętości właściwej i wzrost temperatury) i rozprężaniu gazu (odwrotnie).

Pracę zewnętrzną oblicza się z pierwszej zasady termodynamiki, czyli:

             

Skąd wynika:

             

a po scałkowaniu otrzymujemy:

lz = u1 – u2                                                                                                        (7)

A więc praca zewnętrzna zostaje wykonana kosztem spadku energii wewnętrznej. Wyrażenie (6) można jeszcze przekształcić do postaci:

              .

Ponieważ = R oraz , więc , i następnie

                                                                          (8)

Praca techniczna występuje w drugiej postaci I zasady termodynamiki, czyli można ją obliczyć analogicznie do pracy zewnętrznej. Ponieważ :

             

czyli

             

oraz

l t = i1  –  i2                                                                                          

Jak z powyższego wynika warunkiem wykonania pracy technicznej jest spadek entalpii właściwej [ J/ kg], czyli jest ona wykonana kosztem tego spadku.

Między pracą techniczną i zewnętrzną zachodzi następująca zależność:

              ,

.czyli:                                      lt = k lz

Korzystając  z równania (7) otrzymujemy:

                                                            (9)

  1. Wybrane metody oznaczania wykładnika adiabaty

 

W dalszych rozważaniach rozpatrzymy dwie metody oznaczenia wykładnika adiabaty:

a)      metoda Clementa-Desormesa,

b)      metoda Lummera-Pringsheima.

Pierwsza metoda wymaga prowadzenia pomiaru przy stosowaniu małych nadciśnień gazu, podczas gdy w drugiej ograniczenie to nie występuje. Obie metody wykorzystują matematyczny opis przemiany adiabatycznej w odniesieniu do zmienności ciśnienia, z czego wynika, że podstawowym przyrządem pomiarowym jest manometr cieczowy. 

Opisane niżej doświadczenie spełnia założenie przebiegu przemiany przy małych ciśnieniach ( nadciśnieniach) czyli szukana wartość wykładnika adiabaty może być uzyskana za pomocą procedur obliczeniowych opisujących obie z wymienionych metod.

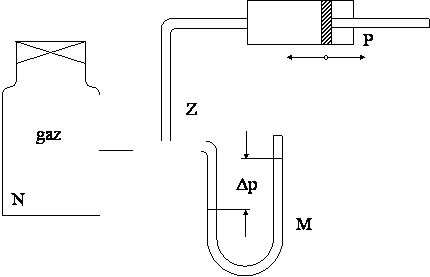
Schemat układu pomiarowego przedstawiono na rys. 3.

 

 

 


                                                                                                                                 

 

 

 

 

 

 

 

 

 

 

 

 


Rys. 3. Schemat układu pomiarowego ( N – naczynie z badanym gazem,

    M – mikromanometr cieczowy, Z – zawór szklany obrotowy,  P – pompka sportowa,

                        Δp  -  mierzone ciśnienie  , mm H2O ).

Badany gaz ( np. powietrze) znajduje się w zamkniętym naczyniu laboratoryjnym. Pierwszy etap pomiaru polega na wtłoczeniu do naczynia niewielkiej ilości tego samego gazu za pomocą pompki sportowej, co powoduje (obserwowany) wzrost jego ciśnienia np. o ok. 100 mm  ( jest to niewielka wartość nadciśnienia, łatwa do pomiaru dowolnym manometrem cieczowym). Sprężanie gazu powoduje wzrost jego temperatury, przy czym z uwagi na krótki czas jego trwania możemy go traktować jako proces adiabatyczny (założenie to nie ma związku a dokładnością dalszych obliczeń) .

Kolejnym etapem, zachodzącym samoistnie, jest izochoryczne oziębianie gazu, zakończone po uzyskaniu zrównania jego temperatury z otoczeniem. Ten etap ( drugi) kończy wstępną część eksperymentu, przy czym jej przebieg  ma znikomy wpływ na dokładność części obliczeniowej.

Dowodem zakończenia tej przemiany jest stabilizacja wskazań manometru.

Badany gaz posiada w tym momencie pewne nadciśnienie. Otwarcie zaworu Z ( rys. 3), powoduje wypuszczenie z naczynia pewnej ilości gazu i jego rozprężenie.  Zawór zamykamy w momencie  zrównania  ciśnienia gazu w naczyniu  z wartością ciśnienia otoczenia. Proces ten trwa ułamek sekundy, co pozwala założyć, że zachodzi on w sposób adiabatyczny. Adiabatycznemu rozprężaniu towarzyszy oziębienie badanego gazu poniżej temperatury otoczenia .

 


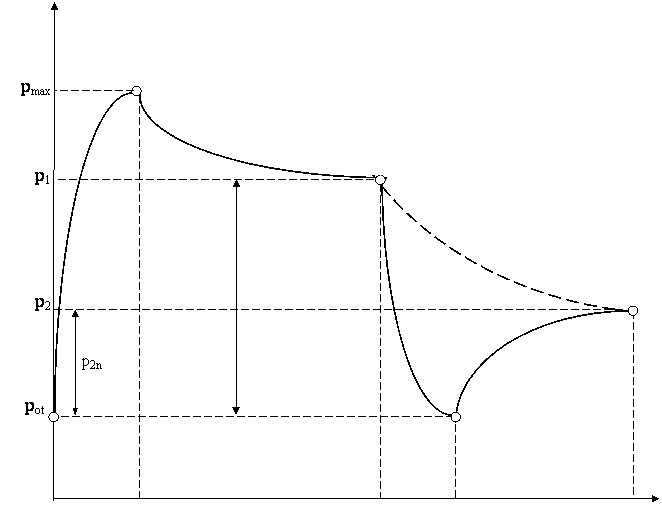
      p

[mm H2O]
 
         

                     B (pmax , T1)

               

                                                                                             

                                                                             

    C( p1, Tot )

                                                                                      

                                               p1n                                                                                                                                                                                                                              E (p2, Tot) 

                                                                                      

 

  

                                                                                                                                D (pot , T2)

A(pot ,Tot)                                                                                                                  

           

              τB                                                     τC        τD                                        τE [s]

            Rys. 4. Krzywa zmiany ciśnienia badanego gazu jako podstawa podziału

   procesu pomiarowego na 4 etapy  (AB -  adiabata,  BC – izochora,

 CD – adiabata,  DE – izochora,  CE – teoretyczna izoterma).

 

W związku z różnicą temperatur gazu w naczyniu i otoczeniu  następuje samoistne izochoryczne podgrzewanie gazu do momentu wyrównania temperatur, czemu towarzyszy  wzrost ciśnienia (p/T = const). Wartość tego wzrostu  (rys. 4) jest zawsze mniejsza w porównaniu z ciśnieniem  początkowym etapu adiabatycznego ( ), co można wyjaśnić zmniejszeniem  masy gazu po otwarciu zaworu w 3.etapie eksperymentu. Przebieg obu procesów adiabatycznych dowodzi, że adiabatyczne sprężanie (linia AB) pociąga za sobą wzrost temperatury gazu, podczas gdy rozprężaniu (CD) towarzyszy spadek temperatury, przy wzroście objętości właściwej zgodnie z równaniem (6).

Zauważając, że dwa ostatnie etapy eksperymentu ( adiabata  połączona z izochorą) odpowiadają przemianie izotermicznej a etap przedostatni – adiabatycznej, należy opisać te procesy z punktu widzenia mierzonych zmian ciśnienia ( nadciśnienia). W obliczeniach tych niezbędna jest znajomość  podstawowej zależności definicyjnej nadciśnienia:

pn = p - pot

gdzie:  pn    -  nadciśnienie mierzone manometrem (cieczowym z rurką pochyłą) ,

            p    -  ciśnienie bezwzględne,

            pot  -   ciśnienie barometryczne.

Podstawowe zależności opisujące ideę obu metod zostaną opisane poniżej.

 

3.    Teoretyczne podstawy obliczania    metodą Clementa.

Do dalszych rozważań niezbędne jest wyrażenie związków pomiędzy ciśnieniem  i objętością gazu w trakcie procesów adiabatycznego  i izotermicznego.

Dla procesu adiabatycznego skorzystamy z następujących zależności:

                  ;

                  ;                     ;

                                                                                     (10)

Równanie izotermy możemy uzyskać jako szczególny przypadek adiabaty dla k = 1, czyli dla przemiany izotermicznej zachodzi związek :

                                                                                        (11)

Wzory (1), (2) w odniesieniu do małej zmiany objętości właściwej   i ciśnienia Δp można zapisać następująco:

a) dla adiabaty:

                                                                                 (12)

b)  dla izotermy:

                                                                                      (13)

Ponieważ  więc:

                

po podzieleniu stronami równań (12) i (13) otrzymamy :

                

                

gdzie:

            p1 , p2                    -  ciśnienia bezwzględne dla punktów pomiarowych 1, 2,

p 1n = p1 – pot      -  nadciśnienie dla punktu 1

 

 

4.  Metoda Lummera - Pringsheima

W szczególnym, najprostszym przypadku przebieg badania może być analogiczny do doświadczenia Clementa-Desormesa. Postać zależności opisującej szukany wykładnik k,  wynika z następujących przekształceń równania adiabaty:

                     lub 

Po zlogarytmowaniu mamy:

                                                                                            (14)

Z równania stanu gazu doskonałego   obliczymy

                                                                                                 (15)

Połączenie zależności (14) i (15) pozwala ująć szukany współczynnik k wzorem:

                                                                                                  (16)

Zgodnie z przebiegiem termodynamicznych etapów doświadczenia [ p = f() - rys. 4] punkty temperaturowe początku (indeks 1) i końca (indeks 2) przemiany adiabatycznej odpowiadają temperaturze otoczenia T1 = Tot (mierzona temperatura powietrza w sali laboratoryjnej) i nieznanej temperaturze końca tej przemiany T2 = Tad. Zależność (16) zapiszemy więc w postaci:

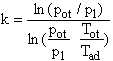                                                                            (17)

Zależność  (17) wyraża metodą Lummera-Pringsheima.

Nieznana temperatura końca etapu adiabaty Tad jest temperaturą początku przemiany izochorycznej (etap IV) zakończonej w momencie uzyskania temperatury otoczenia. Początek izochory odpowiada ciśnieniu otoczenia pot a wskutek pobierania ciepła z otoczenia rośnie ono do wartości p2 ( mierzone manometrem jako p2n ). Tak więc równanie izochory ( p/T = const) pozwala na zastąpienie wartości temperatur za pomocą ciśnień: 

             

Podstawiając wartość Tot / Tad  do (17) otrzymamy wzór końcowy w postaci:

                                                             (18)

5.       Termodynamiczne etapy zastosowanej metody doświadczalnej

 

Kolejność czynności pomiarowych przy oznaczaniu wykładnika adiabaty k (   ) przedstawić można w postaci następujących przemian termodynamicznych:

1)      adiabatyczne sprężenie próbki gazu od  poprzez wtłoczenie do naczynia niewielkiej ilości gazu za pomocą pompki sportowej ( wzrost ciśnienia i temperatury – rys. 4);

2)      samoistne, izochoryczne rozprężanie i stygnięcie gazu w wyniku odprowadzania ciepła do otoczenia, zanikające w momencie wyrównania temperatury gazu i otoczenia,

3)      adiabatyczne rozprężanie i stygnięcie gazu jako skutek celowego, krótkotrwałego otwarcia zaworu oddzielającego (wcześniej) przestrzeń  wewnątrz naczynia od otoczenia ;

4)      samoistne, izochoryczne sprężanie gazu - przy asymptotycznym przebiegu wzrostu ciśnienia – związane z pobieraniem ciepła od otoczenia; przemiana kończy się w momencie osiągnięcia termodynamicznej równowagi (wyrównanie  temperatury gazu i  otoczenia).

 

6.  Przykłady obliczeń dla obu metod badań

Podczas badań uzyskano następujące  nadciśnienia gazu (powietrza) :

  =  90 mm   .

Wg metody Clementa (dla małych nadciśnień)

                

                

Zgodnie z metodą Lummera () :

             

                

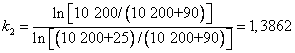
                 Z porównania wartości  wynika bardzo dobra zgodność obu metod dla ma­łych nadciśnień używanych w doświadczeniu. Ponieważ wzór ścisły dotyczy wartości  więc błąd względny wynosi :

                

 

Dla małych wartości 1 mamy

                

oraz

                

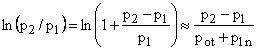
Wtedy uproszczony wzór ma postać:

                 .

 

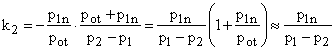Matematyczna postać powyższej zależności wyjaśnia równoważność obu metod oznaczania wartości wykładnika adiabaty k przy zastosowaniu metody małych ciśnień.

 

Arkusz obliczeniowy  znajduje się na  stronie 11 (ostatniej)                                   17.04.2007  

 

 

       Literatura:

1.    B. Staniszewski: Termodynamika. PWN, 1986.

2.    S. Wilk :Termodynamika techniczna, Wyd. Szk. i Pedag. W-wa 1989.

3.    S. Wiśniewski: Termodynamika Techniczna, WNT, W-wa 1987.

4.        Sz. Szczeniowski: Fizyka doświadczalna. Cz. II. Ciepło i fizyka drobinowa. PWN,

       W-wa, 1964.

5.    F. Kohlrausch: Fizyka laboratoryjna. PWN, W-wa 1959.

 

 

 

 

 

 

 

 

 

 

 

 

Imię

Nazwisko

Data

Rok II.    Grupa

 

 

.04.2007

 

Sprawozdanie z ćwiczenia laboratoryjnego nr 7       

Z7 =

„Badanie parametrów przemiany adiabatycznej na przykładzie powietrza”

1.  Dane ogólne dla badanego gazu (powietrza wilgotnego  *):

2.  Obliczenie wykładnika k metodą Clementa (metoda małych ciśnień)

a) obliczenie 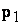i 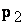 (należy dopasować jednostki składników równania )

b)  obliczenie k

                     

3.  Obliczenie wykładnika k metodą Lummera (dowolne ciśnienie)

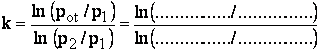 ;    (3 miejsca znacz.np. 1,34)

4.  Określenie temperatury końca przemiany adiabatycznej (etap III) jako początku izochorycznego sprężania gazu przy pobieraniu ciepła z otoczenia (IV etap eksperymentu )

;       

5.    Obliczenie ciepła właściwego cv.pow  i   przyrostu energii wewnętrznej

  ( równanie Mayera )

6.  Obliczenie pracy zewnętrznej (podaj wzór !)

            l z = ……………………… [ J/ kg]

7.  Obliczenie pracy technicznej i zmiany entalpii  (wzór !) 

;             

8.  Teoretyczna wartość wykładnika adiabaty dla powietrza

 ……….

9.   Obliczenie objętości właściwych dla badanej adiabaty ( na odwrocie )

10.  Współczynnik weryfikacyjny  

Jeżeli Z7 nie mieści się w granicach 0.96 ÷ 1.04, to obliczenia należy powtórzyć. Na odwrocie: wnioski, wykres p= f ( τ ), wykres adiabaty (po obliczeniu objętości właściwych υ1 i υ2 ).

Liczba osób posiadających takie same wnioski lub/i  wyniki obliczeń wynosi :  ……

* uwaga:  indeks ‘pow’ oznacza powietrze