Ćwiczenie laboratoryjne nr 4 (w24) 4 . 02.2010

BADANIE PROFILU CIŚNIENIA I NATĘŻENIA PRZEPŁYWU GAZÓW W RUROCIĄGU

1. Wprowadzenie i cel ćwiczenia

Celem ćwiczenia jest poznanie podstawowych praw opisujących przemieszczanie gazu w przewodzie cylindrycznym zwanym rurociągiem. W rozważaniach technicznych podstawowe problemy badawcze dotyczą najczęściej poziomych elementów rurociągu. Badanie kinetyki procesu przemieszczania w rurociągu warunkowane jest koniecznością przeprowadzenia wielopunktowego pomiaru ciśnienia całkowitego i statycznego, uwzględniającego położenie strugi względem osi rurociągu. Parametrem wyjściowym do rozważań kinetyki przepływu czynnika jest rozkład wartości ciśnienia dynamicznego, określany często jako profil ciśnienia.

Pod pojęciem profilu ciśnienia rozumie się pewien rodzaj wykresu ilustrujący jego rozkład przestrzenny w funkcji odległości od osi rurociągu (jest on obrócony o 90^o w porównaniu z matematycznie poprawnym wykresem ciśnienia w funkcji zmiennej położenia). Taki sposób przedstawienia zmienności ciśnienia lub prędkości liniowej jest uzasadniony dążeniem do uzyskania zgodności kierunków odpowiednich wektorów z poziomą osią rurociągu Pod pojęciem płynu rozumie się ciecze lub gazy (również pary).

Analiza wyników badań wymaga znajomości struktury i sensu fizycznego podstawowych parametrów procesu, wynikających przede wszystkim z prawa zachowania energii, znanego w literaturze pod nazwą prawa Bernoulliego.

Przeprowadzone badania pozwalają na:

a) określenie rozkładu zmienności (profilu) oraz wartości średniej ciśnienia całkowitego i dynamicznego,

b) wyznaczenie profilu liniowej prędkości przepływu gazu,

c) analizę ilościową procesu poprzez określenie objętościowego i masowego natężenia przepływu czynnika (gazu).

Celem dodatkowym jest określenie czynników decydujących o profilu prędkości i ciśnienia oraz poznanie fizycznego sensu tzw. bezwymiarowej liczby Reynoldsa, która jest podstawą do klasyfikacji charakteru badanego przepływu. Bardzo ważne jest też rozróżnienie matematycznego modelu procesu w którym uwzględnia się ściśliwość płynu (zwłaszcza dla gazu) od modelu uproszczonego w którym nie zachodzi zmiana gęstości medium (częściej dla cieczy).

Wprowadzone uproszczenia matematyczno-fizycznego modelu procesu są możliwe dzięki założeniu, że przewód badanego rurociągu jest poziomy, prosty i dostatecznie długi. Inne uproszczenia wynikają z faktu, ze przepływający płyn może być ściśliwy lub nieściśliwy.

2. Podstawowe pojęcia i zależności opisujące przepływ gazu

Przepływem nazywamy postępujące przemieszczanie się cieczy, gazów lub par w rurociągach, kanałach, dyszach, przewężeniach oraz innych elementach przewodu. Przepływ nazywa się ustalonym (stacjonarnym), jeśli kierunek i prędkość płynących cząstek w tym samym miejscu strugi jest stała w czasie.

Przykładem takiego przepływu jest wypływająca ze zbiornika woda, której górny poziom nie zmienia się, przez co proces przebiega przy stałej różnicy ciśnień.

W przewodzie o przekroju kołowym, całkowicie wypełnionym przepływającym czynnikiem, wyróżnia się trzy rodzaje przepływów:

a) uwarstwiony (laminarny, warstwowy),

b) przejściowy (mieszany),

b) burzliwy (turbulentny).

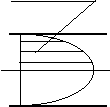
W pierwszym przypadku strugi czynnika przepływającego układają się równolegle do osi przewodu, przy czym w przekroju wzdłużnym rozkład prędkości ma w przybliżeniu kształt paraboli, a największa prędkość przypada w osi przewodu.

Wektory średniej Wektory średniej Wektory średniej

prędkości prędkości prędkości

w_min = 0 w_min = 0 w_min = 0

w_śr = 0.5 w_max w_śr = ~ 0.8 w_max w_śr = ~ 0.85 w_max

Ruch laminarny Ruch burzliwy Ruch burzliwy

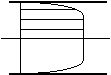
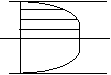
Rys. 1. Schematyczne porównanie przepływu uwarstwionego i burzliwego

( tzw. profile prędkości)

W drugim przypadku cząstki czynnika nie przesuwają się równolegle do przodu, lecz wirują w różnych kierunkach, mieszają się z sobą tworząc rodzaj linii śrubowej. Rozkład prędkości przedstawia krzywą spłaszczoną, przy czym w środkowej części, przewodu prędkość pozostaje ta sama, a od pewnego miejsca zmniejsza się znacznie aż do zera przy ściance przewodu (rys. 1). Również przy przepływie burzliwym ruch czynnika można określić jako prostoliniowy, gdy za prędkość strumienia przyjmuje się średnią prędkość przepływu. Rysunek 1 podaje dwa przykłady ruchu burzliwego, które pokazują charakter spłaszczonej krzywej rozkładu prędkości.

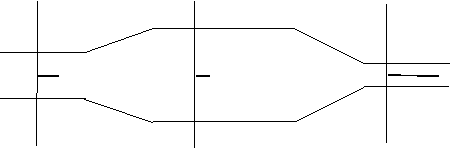
Rozpatrując następnie dowolnie długi odcinek przewodu o zmiennych przekrojach, zakłada się analogicznie, że do każdego przekroju dopływa i odpływa na sekundę ta sama masa czynnika i że wszystkie przekroje są wypełnione czynnikiem, a więc nie powstają żadne puste miejsca (rys. 2).

F₁ F₂ F₃

w₁, v₁, T₁ w₂, v₂, T₂ w₃, v₃, T₃

I II III

Rys. 2. Schemat przepływu w przewodzie o zmiennym przekroju

Zakładając, że przepływający płyn (ciecz lub gaz) nie zmienia swojej temperatury oraz przepływa w kanale poziomym, czyli różnice wysokości nie mają wpływu na przebieg procesu. Kinetykę przepływu płynu (gazu) w rurociągu opisują dwa podstawowe parametry:

a) objętościowe natężenie przepływu:

b) masowe natężenie przepływu:

gdzie :

– masowe natężenie przepływu , tj. masa przepływającego czynnika odniesiona do jednostki czasu [ ],

– objętościowe natężenie przepływu , tj. objętość przepływającego czynnika odniesiona do jednostki czasu .

Poniższe rozważania wynikają z bilansu masy, stanowiącego (zdaniem a.) termofizyczną odmianę prawa zachowania masy (w aspekcie praktycznym „prawo szczelności rurociągu”).

Fundamentalnym parametrem wyrażającym ten bilans jest tzw. masowe natężenie przepływu, jednakowe dla każdego przekroju (I, II i III - rys. 2), które wyrazimy wprowadzając parametry:

F - powierzchnię przekroju przewodu w dowolnym miejscu, ,

p - ciśnienie bezwzględne, ,

g - przyspieszenie ziemskie, ,

w - średnią prędkość przepływu w badanym miejscu przewodu, ,

υ - objętość właściwą przepływającego czynnika, ,

r - gęstość czynnika przepływającego (r = 1/ υ) , .

Masowe natężenie przepływu można wyrazić dwoma, równoważnymi sposobami :

(1a)

lub

(1b)

Podstawowe i ogólne równania (1a, 1b) można niekiedy uprościć, zakładając rozważania dla przypadku cieczy nieściśliwych oraz - mniej dokładnie - dla gazów i par w kanałach o niewielkiej zmianie powierzchni przekroju F. Można wówczas przyjąć niezmienność objętości właściwej (również gęstości!) , co pozwoli uzyskać:

[ m³/ s ] (2)

lub ogólnie

[ m³ / s ] (3)

Jest to tzw. zasada ciągłości przepływu, dotycząca cieczy nieściśliwych. Stwierdza ona, że w dwu dowolnych miejscach przewodu prędkości są odwrotnie proporcjonalne do powierzchni

przekrojów. Jeżeli więc strumień natrafia na zwężenie rurociągu lub kanału, jego prędkość powinna się zwiększyć, aby ta sama ilość czynnika przepłynęła w jednostce czasu. Przeciwnie zaś, gdy przekrój się zwiększa, wówczas prędkość przepływu się zmniejsza. Identyczne wnioski wynikają oczywiście z równania ogólnego (1a, 1b).

Zwiększenie się prędkości w czasie przepływu, a tym samym energii kinetycznej w zwężającym się przekroju rurociągu, jak np. na rys. 2, może się odbywać tylko kosztem energii potencjalnej. Należy pamiętać, że rozważania te dotyczą wyłącznie przypadku, gdy w rurociągu płynie ciecz nieściśliwa oraz przemieszczanie się czynnika odbywa się bez tarcia.

Rozpatrując bilans energii zauważymy, że całkowita energia przepływającej cieczy składa się z energii cieplnej, energii kinetycznej przepływu oraz energii potencjalnej, przy czym tę ostatnią stanowi energia ciśnienia i energia położenia. Dla lepszego zobrazowania wszystkich rodzajów energii, zakłada się, że rozpatrywany odcinek przewodu nie jest nachylony do poziomu, a zmiany energii cieplnej są pomijalnie małe. Stosując prawo zachowania energii do przepływającego elementu o objętości , otrzymuje się wyrażenie

(5)

energia położenia + energia ciśnienia + energia kinetyczna = const

(uwaga: nie należy mylić: p i ρ !)

Podzieliwszy obydwie strony równania (5) przez , otrzyma się inną postać równania Bernoulliego, będącą bilansem ciśnień:

(6)

Poszczególne człony oznaczają:

- wysokość geodezyjna położenia,

p - ciśnienie statyczne lub hydrostatyczne,

- ciśnienie dynamiczne.

Z podanych wzorów (5, 6) wynika, że w całej długości rurociągu suma energii lub wyznaczających ją parametrów pozostaje zawsze wartością stałą. Zmiana jednego członu powoduje odpowiednią zmianę członów pozostałych.

Ze względu na to, że w praktyce przewody są poziome lub bardzo zbliżone do poziomu, czyli , można opuścić pierwszy człon równań (5, 6), uzyskując równanie:

(7)

Ze wzoru ( 7 ) widać, że zwiększenie się prędkości powoduje obniżenie ciśnienia i odwrotnie. Równanie (7) wygodnie jest zapisać w postaci :

(8)

Ponieważ każdy z członów powyższego wzoru ma wymiar ciśnienia, więc taki sam wymiar powinna również mieć suma, którą oznacza się jako ciśnienie całkowite .

Człon pierwszy równania będziemy nazywać ciśnieniem statycznym , natomiast człon drugi 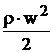ciśnieniem dynamicznym . Z powyższych rozważań wynika bardzo ważna dla procedury badań doświadczalnych zależność :

(9)

Wyznaczona z wartości ciśnienia dynamicznego liniowa prędkość przepływu wynosi:

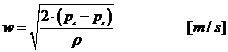(10)

lub

(11)

Ciśnienie całkowite p_c [ Pa ] mierzy się rurką zgiętą, skierowaną przeciw prądowi, tzw. rurką Pitota, podłączoną do manometru ( np. cieczowego). Ciśnienie mierzone idealną rurką Pitota, przy prędkości poniżej prędkości głosu i niezbyt małych liczbach Reynoldsa, nazywa się ciśnieniem Pitota. Ciśnienie statyczne p_s [ Pa ] mierzy się rurką prostą umieszczoną prostopadle do kierunku przepływu .

Ciśnienie dynamiczne p_d , z którego oblicza się prędkość w, jest więc różnicą zmierzonego w powyższy sposób ciśnienia całkowitego i statycznego.

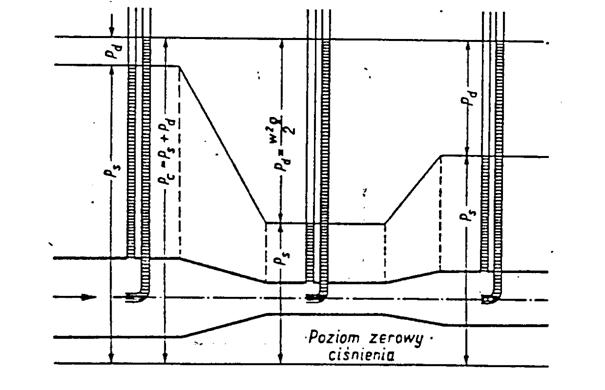
Rys. 3. Schemat rozkładu ciśnień w czasie przepływu (nie obowiązuje!)

Na rys. 3 pokazano zmiany energetyczne, przedstawiane jako zmiany ciśnienia w czasie przepływu w przewodzie o zmiennym przekroju. Widoczne jest, że ciśnienie całkowite pozostaje bez zmian, natomiast zmienia się ciśnienie statyczne, a tym samym dynamiczne. W przekroju węższym obniża się ciśnienie statyczne, a podwyższa się ciśnienie dynamiczne, gdyż zwiększenie prędkości odbywa się kosztem spadku ciśnienia albo energia kinetyczna zwiększa się kosztem zmniejszenia się energii potencjalnej i odwrotnie.

Mając zmierzone średnie ciśnienie dynamiczne w danym przekroju, można określić objętościowe natężenie przepływu czynnika (płynu), wstawiając do równania (2) wprowadzone wzory (10) i (11):

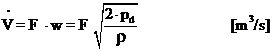(12)

Dla masowego natężenia przepływu otrzymuje się zależność:

(13)

Z przedstawionych zależności wynika, że dla określenia kinetyki przepływu czynnika (gazu) konieczne jest wyznaczenie profilu ciśnienia dynamicznego, obliczenie średniej prędkości liniowej i wyznaczenie powierzchni wewnętrznego przekroju rurociągu (przewodu).

3. Przykład obliczeniowy

Rozpatrujemy przemieszczanie się gazu w poziomym przewodzie, posiadającym trzy zmienne przekroje (rys. 4). Rurociąg jest szczelny, więc do każdego przekroju dopływa i odpływa ta sama masa gazu w odniesieniu do jednostki czasu. Wszystkie przekroje są całkowicie wypełnione czynnikiem. Z warunków zadania wynika konieczność uwzględnienia zmiany gęstości [ ρ ] i objętości właściwej [ υ ] gazu dla różnych przekrojów, co może być konsekwencją zmian ciśnienia i temperatury. Dla trzech przekrojów określono następujące parametry przepływu:

F₁ = 0,5 m² , w₁ = 2 m /s, υ₁ = 0,8 m³/kg,

F₂ = 2,4 m² , w₂ = 0,4 m /s,

F₃ = 0,3 m² , υ₃ = 0,75 m³/kg.

Należy obliczyć:

a) gęstość i objętość właściwą gazu w przekroju 2,

b) liniową prędkość przepływu w przekroju 3,

c) masowe natężenie przepływu.

Przekrój 1 Przekrój 2 Przekrój 3

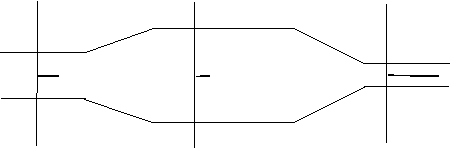
w₁ , υ₁ , F₁

w₂, υ₂, F₂ υ₃, F₃

Rys. 4. Parametry przepływu dla przewodu o zmiennych przekrojach (zmienne υ, ρ, w).

UWAGA: W tym przypadku absolutnie błędną jest zależność:

F₁ w₁ = F₂ w₂ = F₃ w₃ , bo zmienna jest objętość właściwa !!

Podstawowa zależność, stanowiąca termofizyczną mutację prawa zachowania masy, ma postać :

lub

Obliczamy kolejno :

Objętość właściwa: υ₂ = 0,4 ^. 2,4 / ( 0,5 ^. 2) ^. 0,8 = 0,768 m³ /kg

Gęstość: ρ₂ = 1/ υ₂ = 1/ 0,768 = 1,302 kg/ m³.

Prędkość liniowa w₃ = F₁ w₁ υ₃ /( F₃ υ₁) = 0,5 ^. 2 ^. 0,75/ (0,3 ^. 0,8) = 3,12 m/ s.

Masowe natężenie przepływu :

1,25 kg/ s.

4. Zasada działania manometru cieczowego dwuramiennego

Elementarnym przyrządem do pomiaru ciśnienia jest rurka szklana, wygięta w kształcie litery U, posiadająca pionowe ramiona częściowo wypełnione cieczą manometryczną o znanej gęstości ρ_m. Jest to najprostszy manometr cieczowy.

Manometr ten mierzy różnicę ciśnień działających na swobodne powierzchnie cieczy w rurkach. Przyjmiemy, że indeksy 1 , 2 dotyczą parametrów gazów znajdujących się w U-rurce powyżej cieczy manometrycznej.

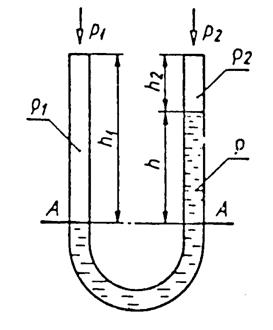
Rys. 4. Manometr cieczowy dwuramienny

W bilansie - odniesionym do przekroju A-A ( rys. 4) - porównamy sumę sił działających w lewym ramieniu manometru (lewa strona równania) z sumą sił działających w prawej części manometru, wśród których występuje, miarodajna dla mierzonej różnicy ciśnień, wysokość h. Indeksem „m” oznaczono dane odnoszące się do cieczy manometrycznej ( najczęściej woda). Bilans ten ma postać :

(19)

Gęstość gazu jest zawsze znacznie mniejsza od gęstości cieczy. Jeśli więc gęstości i są zbliżone do siebie i mniejsze od ρ_m (np. gdy w obu ramionach rurki ponad cieczą manometryczną znajduje się powietrze, czyli ρ₁ << ρ_m oraz ρ₂ << ρ_m ), to wzór upraszcza się do postaci:

(20)

Wzór (20) jest bardzo przydatny do przeliczania jednostek wyrażonych w postaci wysokości słupa cieczy manometrycznej na Pascale, np.

1 mm H₂O = 1000 kg/m^{3 .} 9,81 m/ s^{2 .} 0,001 m = 9,81 N/ m² = 9,81 Pa

5. Pomiar natężenia przepływu gazu za pomocą rurki Pitota i Prandtla

Najprostszym przyrządem do pomiaru ciśnienia dynamicznego jest połączenie rurki zgiętej, właściwej rurki Pitota, mierzącej ciśnienie całkowite, z rurką prostą, mierzącą ciśnienia statyczne. Układ ten często niewłaściwie zwany jest także rurką spiętrzającą Pitota. Udoskonaloną postacią tego połączenia jest rurka spiętrzająca Prandtla (rys. 5), zaprojektowana dzięki pomiarom aerodynamicznym w celu osiągnięcie współczynnika korekcyjnego równego 1.

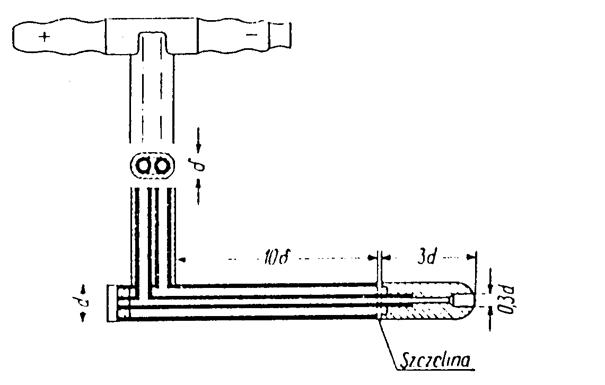
Rys. 5. Rurka Prandtla

Rurka Prandtla ma w części cylindrycznej szczelinę do pomiaru ciśnienia, w takiej odległości od czoła, aby strugi można było uważać za równoległe. Zamiast szczeliny można wykonać kilka lub kilkanaście okrągłych otworków. Mierzone tutaj ciśnienie odpowiada ciśnieniu statycznemu przepływającego czynnika. Szczelina wykonana jest w rurce zewnętrznej, w której znajduje się druga rurka. Czoło drugiej wewnętrznej rurki, skierowane przeciw prądowi, jest zaokrąglone i ma otwór wynoszący 0,3 średnicy zewnętrznej rurki, który to otwór jest miejscem pomiaru ciśnienia całkowitego. Obydwie rurki pomiarowe są wyprowadzone na zewnątrz i przyłączone do manometru różnicowego (np. do rurki U), który w tym przypadku pokazuje wprost ciśnienie dynamiczne .

Wobec tego, że rurka Prandtla nie odpowiada warunkom przyrządów ruchowych, więc tych rurek nie umieszcza się na stałe, lecz używa się tylko do doraźnych kontrolnych pomiarów gazów o niskim ciśnieniu. Przy ciśnieniach wyższych mogą powstać trudności przy uszczelnianiu i wykonywaniu pomiaru m.in. z powodu zanieczyszczania się otworów do pomiaru ciśnień. Ponadto rurka Prandtla przy niedużych prędkościach stosowanych w praktyce daje małe spiętrzenia, a tym samym małą dokładność pomiaru.

Na rys. 6 pokazano sposób pomiaru za pomocą rurki Prandtla w przewodzie, w którym przepływa gaz o ciśnieniu niewiele wyższym od otoczenia. Zasadniczo należy wykonać kilka pomiarów wzdłuż powierzchni przekroju w celu oznaczenia średniej prędkości. Chcąc się ograniczyć tylko do jednego pomiaru, należy czujnik rurki Prandtla ustawić w takim miejscu, gdzie, prędkość przepływu jest średnia dla całego przekroju. W praktyce dla przepływów burzliwych, z którymi ma się prawie wyłącznie do czynienia, nie popełnia się dużego błędu, jeśli czujnik umieszczony jest w odległości ok. 0.3 D od powierzchni wewnętrznej rurociągu.

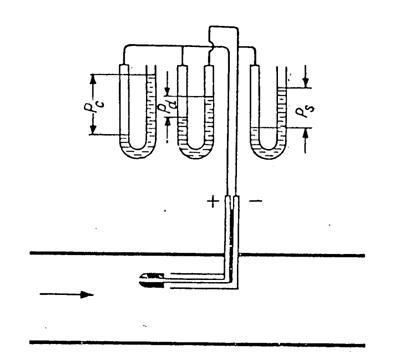
Rys. 6. Schemat pomiaru ciśnienia całkowitego, statycznego i dynamicznego rurką Prandtla

( p_d = p_c - p_s , nie obowiązuje !)

Ciśnienie dynamiczne p_d mierzy się za pomocą rurki dwuramiennej („U”) lub innych manometrów cieczowych (np. Recknagla). Możemy też wykonać osobny pomiar ciśnienia całkowitego i statycznego, zgodnie ze schematem na rys. 6. Ponieważ mierzone ciśnienia wykazują niewielkie wartości do pomiarów korzystnie jest używać rurek U pochyłych (Recknagela).

6. Opis przebiegu badań

Schemat metody badań ciśnienia całkowitego i statycznego przedstawiono na rys. 7.

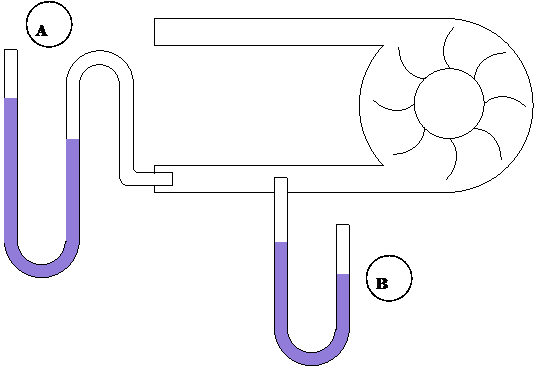
Rys. 7. Schemat badań ciśnienia całkowitego (A) oraz ciśnienia statycznego (B).

Badania profilu ciśnień przeprowadza się dla czterech wybranych punktów przekroju rurociągu tj. w odległościach od ścianki 0.06 D, 0.3 D, 0.4 D oraz 0.5 D. W każdym z nich przeprowadza się za pomocą rurki Pitota pomiar ciśnienia całkowitego i rurką prostą ciśnienia statycznego. Kolejność obliczeń do określenia profilu prędkości i natężenia przepływu jest następująca:

1. określenie ciśnienia barometrycznego, temperatury powietrza i średnicy wewnętrznej rurociągu ( 45 mm),

2. określenie indywidualnej stałej gazowej i lepkości kinematycznej gazu,

3. obliczenie gęstości ( ρ ) i objętości właściwej ( υ ) powietrza,

4. wyznaczenie dla badanych punktów wartości ciśnień dynamicznych i wartości lokalnej prędkości liniowej gazu,

5. określenie charakteru przepływu gazu według obliczonej wartości liczby Reynoldsa,

6. wyznaczenie średniej prędkości gazu w badanym przewodzie,

7. określenie objętościowego natężenia przepływu,

8. obliczenie masowego natężenia przepływu gazu,

9. sporządzenie wykresów profilu ciśnienia i profilu prędkości.

Z przedstawionej metody badań wynika procedura obliczeń zawarta w arkuszu sprawozdawczym ( str. 11).

UWAGA: Przykłady zadań dotyczących przepływu w rurociągu posiadają studenci grupy 3.

7. Zagadnienia do kolokwium z tematu

” Badanie profilu ciśnienia i natężenia przepływu gazów w rurociągu ”

1. Równanie Bernoulliego, zależności definiujące pojęcia ciśnienia całkowitego, statycznego i dynamicznego.

2. Schemat pomiaru ciśnienia całkowitego i statycznego oraz wyznaczanie średniej prędkości liniowej.

3. Podaj zależności opisujące zmienność masowego natężenia przepływu dla rurociągu o zmiennej powierzchni przekroju dla płynów ściśliwych i nieściśliwych.

4. Mając dane dla dwu przekrojów rurociągu : F₁ = 0,2 m² , ρ₁ = 1,2 m³/ kg, m₁* = 2,4 kg/ s

.oraz F₂ = 0,4 m² , w₂ = 6 m /s, obliczyć:

.w₁ , υ₁ , V₁*, υ₂ , V₂*, m₁* ( Uwaga: * zastępuje kropkę nad: m lub V).

Uwaga : υ - objętość właściwa, ρ – gęstość.

5. Podaj kryterium pozwalające na określenie charakteru przepływu.

6. Podstawowe jednostki ciśnienia i ich przeliczanie.

7. Jaki parametr wymaga zastosowania równania stanu gazu?

8. Przedstawić zasadę działania manometru cieczowego dwuramiennego ( tzw. U-rurka)

9. Wyjaśnić pojęcia nadciśnienia i podciśnienia.

---------------------------------------------------------------------------------------------------------

K o n i e c

Na kolejnej stronie przedstawiony jest arkusz sprawozdania.

Opracował : dr inż. A. Gradowski

	Imię	NAZWISKO	Data pomiaru	Techn. cieplna Rok II (W24)
			29. 10. 2009	Grupa 1 2 3
Zw =

Sprawozdanie z ćwiczenia laboratoryjnego nr 4

”Badanie profilu ciśnienia i natężenia przepływu gazów w rurociągach”

1 . Podstawowe parametry badanego gazu ( powietrza )

p_b = p_ot = ……………………………..

t_ot =..……^oC (15 – 25) ; n_pow = (ind. stała gaz. dla powietrza)

D = 45 mm = ............ m. (średnica wewnętrzna rurociągu). UWAGA: nie mylić lepkości „n” z obj. właściwą υ!

2. Obliczenie gęstości powietrza wg równania stanu gazu

a) ciśnienie absolutne z uwzgl. średniego ciśnienia statycznego p_s ( wg tabeli 3, dopasuj jednostki wg wzoru p = ρ g h ^##)

b) obliczenie gęstości (ρ) i objętości właściwej (υ) powietrza

ρ_pow = p / ( RT ) = ……….../ …………… = ………. [ kg/ m³]

υ_pow = 1/ ρ_pow = .../ …..… = …… [ m³ / kg ]

3. Wyniki pomiarów ciśnienia całkowitego i statycznego mikromanometrem Recknagela (w mm H₂O)

S = x / D	0.06	0.3 *	0.4	0.5
P c [mm H2O]
P s [mm H2O]
P d [ Pa]^##
w [m/s]
Uwagi		wśr (Re = …..……)

* jeżeli Re > 50000, to kolumna dotyczy wartości średnich ; x –odległość od powierzchni wewnętrznej

4. Określenie charakteru przepływu wg liczby Reynoldsa (w_sr – pr. średnia, ν_pow – lepkość kinematyczna)

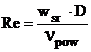= ............................. / ..................... = ................... (3 miejsca znacz. np. 28500)

Charakter przepływu jest: laminarny /przejściowy/ burzliwy ?? niepoprawne skreślić (2320, 50000, Walden)

5. Obliczenie objętościowego natężenia przepływu

a) powierzchnia wewnętrznego przekroju rurociągu F = 3.14 ^....................... = .............. [ m²]

b) objętościowe natężenie przepływu (podaj wzór i podstaw dane !) :

= …………………................................................................. = ................... [ m³ /s ]

c) masowe natężenie przepływu m (podaj wzór i podstaw dane !) :

= ............................................................................................. = ………… [ kg / s ]

6. Współczynnik weryfikacyjny ( sens kontrolno- dydaktyczny)

Z_w= r _pow / 1.2 + w_śr / 30 = ................/ 1,2 + ................/30

Z_w = ................ ( 2 miejsca znaczące np. 2,7 )

Na odwrocie: funkcja lub profil ciśnienia dynamicznego, profil prędkości, spraw. wybranych jednostek i wnioski.

Liczba studentów mających takie same ( jak wyżej podane) wyniki : … Termin oddania: 14 dni (w24-2010)